
백터 기본 개념정리

벡터는 크기 & 방향을 모두 가진 수량을 뜻한다.
그리고 세기(힘), 변위, 속도를 가지고 있는데, 이는 3차원에서 플레이어가 바라보는 방향등을 의미하고 한다.
그리고 벡터는 기본적으로 지향선분으로 표시를 한다.
여기서 지향선분이란? 시각적으로 벡터는 방향이 있는 선분으로 표시를 하는데 이를 뜻함.
위에 사진에서 보듯, 화살표는 벡터의 방향을 가리키며, 선분의 크기는 벡터의 크기를 나타낸다.
그리고 이 기다린 화살표(벡터)가 위치가 바뀌어도 딱히 별로 중요하지 않는데,
이는 벡터가 있는 위치를 바꾼다고 해도 벡터의 성질(선분의 길이, 방향)은 변하지 않기 때문이다.

이렇게 벡터 u를 이동해서 v와 완전히 겹치게 된다면 이 둘을 구분을 할 방법이 없다.
이유는 둘다 성질이 같은 상등이기 때문이다.
때문에 백터는 위치와 무관하며, 단지 어디로 가는지만 나타낼 뿐이다.
벡터의 좌표계(공간)

하지만 좌표계가 있다면 이야기가 달라진다.
일단 벡터는 기하학 연산을 정의해서 벡터값 수량으로 관여하는 문제를 풀때 매우 용이하다.
하지만 우리가 벡터를 이용하는 곳은 바로 컴퓨터이다.
컴퓨터는 벡터를 기하학적으로 다루지 못하기 때문에 이 벡터를 수치화할 방법이 필요하다.
그 수치화를 하는 방법은 바로 좌표계를 만드는 것.
위 그림처럼 공간에 하나의 3차원 좌표계(X,Y, Z)를 도입하여
모든 벡터를 그 꼬리가 그 좌표계의 원점과 일치하도록 이동하는 것이 그 방법이다.
지금 보면 V는 꼬리가 좌표의 원점과 일치하도록 위에 있는 V를 아래로 옮겼다.
그러면 꼬리가 X,Y,Z의 원점과 일치해 있는데, 이를 우리는 "표준위치"에 있는 벡터라고 한다.
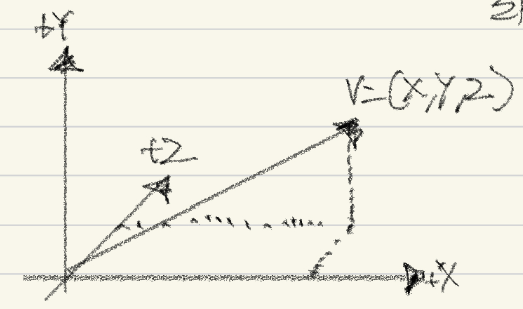
이렇게 하면 하나의 벡터를 그 머리의 끝(화살표 긑)의 좌표로 규정이 가능하다.
또한 우리는 이를 식으로 나타낼 수도 있다. v=(x,y,z)라고 말이다.
이렇게 되면 컴퓨터에서 부동 소수점(float, double)을 이용하여 계산이 가능하다.

위에 사진에 있는 기준계는 내가 배우는 책에서 좌표계, 공간이라고 할때와 모두 같은 말이다.
즉, 기준계 = 좌표계 = 공간이라는 뜻.
일단 벡터를 수치적으로표현 하려면 위에 말한대로 표준위치에 있어야 한다.
위의 그림의 경우 벡터 v의 꼬리를 기준계(좌표계) A의 원점으로 이동할 수도 있고,
옆에 B의 기준계(좌표계)로도 이동이 가능하다.
우리가 눈여겨 봐야할 것은 A를 기준으로 한 백터 v의 좌표와 B를 기준으로 한 v의 좌표가
다르단 것을 주목을 해야 한다.
A의 경우 v = (x,y)이지만, B의 경우는 v = (x', y')이다.
한마디로 같은 벡터 v라고 해도, 기준계(좌표계)가 다르면 그 좌표에 대한 표현이 달라진다.
좌표계가 없을 때는 벡터의 위치가 변하는게 상관이 없지만,
서로 성질이 다른 두개의 좌표계가 있을경우 벡터가 위치한 좌표계의 성질에 따라 방향이 바뀔수 있다는 뜻.
화살표 선분에 내포도니 벡터의 방향, 크기는 변하지는 않지만,
좌표계에 따라 바뀌는건 벡터를 표현하는 좌표 뿐이다.
즉, 좌표는 절대적인 수치가 아니고, 기준계에 상대적인 위치이다.
그리고 그 예시가 왼손 좌표계, 오른손 좌표계이다.
이건 다음에 블로그에 남기도록 하겠다.
댓글